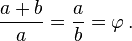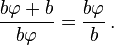شیارهای ناپیدا.....
اگنس مارتین نقاش کانادایی که معمولا آثارش مینیمال شمرده میشود و خود را اکسپرسونیست انتزاعی میدانست. آثار او ترکیبی از شیارهای تقریبا ناپیدا بود که بر زمینه? ساده و تک رنگ نقش میانداخت.
مارتین در بین سالهای 1941 تا 1954 در دانشگاه کلمبیای نیویورک درس خواند و در اواخر دهه پنجاه و دهه شصت با کلی، روزنکیست و دیگر هنرمندان جوان نیویورک مراوده برقرار کرد ،از سال 1967 در کوبا و نیومکزیکو در انزوا زیست و البته از سال 1958 به بعد نمایشگاههایی انفرادی و گروهی برگزار کرد .این هنرمند نقاش از جمله پیروان برجسته اکسپرسیونیسم انتزاعی و بعدا از پیشروان مینیمال آرت می باشند.
اصطلاح مینیمالیسم در قرن بیستم به ویژه در دهه 1960 برای توصیف سبکی به کار رفت که ویژگی آن بی پیرایگی فوق العاده ،شکل بندیهای هندسی ساده و بهره گیری از مواد و مصالح صنعتی بود. پیروان این جنبش از انواع ساختارهای مدولی ، فضایی،شبکه ای و جفتگاری استفاده می کردند و می خواستند در برابر تهییج کنندگی و عاطفه برانگیزی اکسپرسونیسم انتزاعی واکنش نشان دهند.آثار مارتین از درخشان ترین نمونه های مینیمالیستی است.

هنر مدرن_نوربرت لینتن
[ دوشنبه 92/9/11 ] [ 12:27 عصر ] [ علیرضا حسینی ]
اندی وارهول
هنر پاپ، هنری کمابیش طاغی و ضد ارزشهای هنری آکادمیک بود که در میانه? قرن بیستم پا گرفت. آثار اندی وارهول یا اندرو وارهولا با وجود آنکه در زمان حیاتش مخالفان بسیاری در میان منتقدان داشت محبوبیت عام زیادی کسب کرد و او را به یکی از جنجالیترین شخصیتهای هنری مبدل کرد. هماکنون بزرگترین موزه? دنیا که به یک هنرمند اختصاص دارد در پیتزبورگ پنسیلوانیا موزه? اندی وارهول است.
زنگی نامه
اندی وارهول در 6 اوت 1928 (میلادی) در پنسیلوانیا به دنیا آمد. او فرزند سوم یک خانواده کارگر مهاجر بود.
وارهول در سالهای 1960 استودیوی معروف خود را با نام «کارخانه» (The Factory) تأسیس کرد. او با این کار ویژگی یکتایی و ناب بودن اثر هنری را از بین برده و شروع به تولید آثار هنری در مقیاس انبوه کرد. در همین دوره وارهول شروع به نقاشی از تولیدات معروف آمریکایی مانند سوپ کمپبل و بطری کوکاکولا نمود. یکی از شناخته شدهترین کارهای او، قوطیهای سوپ کمپبل است که در سال 1962 میلادی ترسیم شده است.
او در کتاب «فلسفه اندی وارهول» نوشتهاست: «چیز شگفت انگیز درباره آمریکا این است که سنتی را آغاز کرده که در آن ثروتمندترین مشتریان دقیقا همان چیزی را میخرند که فقیرترینشان. شما میتوانید کوکاکولا را در تلویزیون ببینید و میدانید که رئیس جمهور کوکاکولا میخورد، الیزابت تایلور کوکاکولا میخورد، و فکر کنید، شما هم میتوانید کوکاکولا بخورید. کوکا همان کوکاست و با هیچ مقداری از پول نمیتوانید کوکایی بهتر از آنچه داشته باشید که یک ولگرد در گوشهای میخورد. همه کوکاها یکسان هستند و همه آنها خوب. این را الیزابت تایلور میداند، رییس جمهور میداند، ولگرد میداند و شما هم میدانید.» از ویژهترین شیوههای وارهول تکرار است، او با استفاده از چاپ سیلک برای تکرار مکانیکی موضوعاتش و حذف احساسات شخصی هنرمند از اثر، زندگی و تصویرهای زندگی انسان مدرن را به نمایش میگذارد.
او در 22 فوریه 1987 در نیویورک درگذشت و آنجا به خاک سپرده شد.






[ دوشنبه 92/9/11 ] [ 12:17 عصر ] [ علیرضا حسینی ]
قوطیهای سوپ کمپبل
قوطیهای سوپ کمپبل (1962 میلادی) بدون تردید مشهورترین اثر نقاش معاصر آمریکایی، اندی وارهول (1928 - 1987 میلادی) است.
زمانی که وارهول برای اولین بار این 32 عدد طرح را به نمایش گذاشت، همه آنها درست مثل نحوه قرار گرفتنشان در یک سوپرمارکت همزمان در کنار هم به دیوار آویخته شده بودند. این 32 عدد طرح به دلیل تعداد 32 عدد کنسرو مختلف با طعمهای گوناگون که در شرکت کنسروسازی کمپل در زمان شکلگیری اثر (سال 1962) تولید میشده، انتخاب شدهاست.
نکته قابل توجه در این اثر، طعم و بوی مختلفی است که نقاش با شیوهای ویژه به هر کدام از این تابلوهای کوچک با توجه به نوع کنسرو اختصاص دادهاست و آرایش منحصر به فردی در چیدمان این قوطیها کنار یکدیگر تا به امروز کشف نشدهاست. وارهول قوطیها را با توجه به تاریخ معرفی و تولید آنها توسط شرکت کمپبل به ترتیب قرار دادهاست، برای نمونه کنسرو سوپ گوجهفرنگی اولین محصولی است که در سال 1897 میلادی توسط شرکت کمپبل تولید شد و در بالا سمتِ چپ اثر دیده میشود.
وارهول از طرفداران عدم مرزبندی هنر برای قشری خاص با علایقی بعضا پوسیده و تکراری بود و آن را برای تمام مردم، از هر قشر و طبقهای میپسندید. همین دیدگاه منحصر به فرد اندی وارهول باعث شکلگیری تعریفی جدید از هنر مدرن با عنوان پاپ آرت (به انگلیسی: Pop Art) یا هنر مردمی شد. این اثر هم اکنون در موزه هنر مدرن (MoMA) در نیویورک نگهداری میشود.
منابع
Wikipedia contributors, «Campbell"s Soup Cans,» Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Campbell%27s_Soup_Cans&oldid=173784183 (accessed November 27, 2007)
[ دوشنبه 92/9/11 ] [ 12:15 عصر ] [ علیرضا حسینی ]
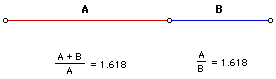
ایجاد نسبت طلایی عبارت است از تقسیم پاره خط به دو قسمت به طوری که نسبت طول قطعه بزرگ تر به طول تمام پاره خط، مساوی با طول قطعه کوچک تر به قطعه بزرگ تر باشد. این نسبت در قدیم به تقسیم خط به نسبت ذات وسطین و طرفین (یا تقسیم توافقی) معروف بوده است که معادل آن به صورت اعشاری در حدود 1.618 خواهد بود که این عدد همان عدد فی می باشد و یکی از خواص آن این است که اگر یک واحد از آن کسر کنیم مقدار آن برابر عکس خودش می شود.
نتایج تحقیقات فراوان علمی و روان شناسی اعلام می کند که زیباترین سطوح و اشکال از نظر انسان ها، آنهایی هستند که در ابعاد آنها نسبت طلایی به کار رفته باشد.

نویسندگان رنسانس این تناسب را نسبت آسمانی و پیروان اقلیدس آن را ذات وسطین و طرفین می خواندند و از قرن 19 بعد بعد این تناسب در بین هنرمندان به نام تقسیم طلایی معروف گشت. در دوره رنسانس مطالعه در مورد این نسبت در بین ریاضی دان ها معمول بوده است. به طوری که کاکستر در اول مقاله خود به نقل از کپلر می نویسد: هندسه صاحب دو گنجینه بزرگ است، یکی قضیه فیثاغورث و دیگری تقسیم خط به نسبت ذات وسطین و طرفین که اولی را می توان با طلا مقا یسه کرد و از دومی به عنوان یک گوهر گران بها اسم برد.
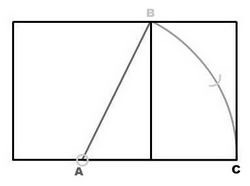
نحوه ترسیم هندسی مستطیل طلایی به کمک مربع
این نسبت از قدیم در بین هنرمندان و معماران شناخته شده و در آثار خود از آن استفاده می کرده اند؛ نظیر ساختمان معبد پارتنون که در آن این نسبت به کار رفته است.

در اهرام مصر نیز این نسبت به دقت رعیات شده است. مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم!
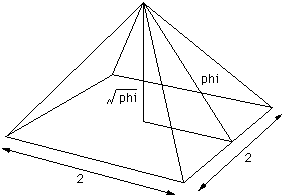
 مدارک به دست آمده از دو هزارسال قبل از میلاد در یکی از اهرام مصر نیز که در یکی از اطاق ها تصویری به دست آمده، حاکی از مطالعه این نسبت روی اجزای بدن انسان است که مطالعه آن توسط لوکوربوزیه معمار فرانسوی روی بدن انسان، جدول معروفی را به دست می دهد که با استفاده از قابلیت تقسیم طبیعی در بدن انسان، علم نسبت ها را در ساختمان وارد کرده است. بررسی های لوکوربوزیه بعد از وی توسط دیگر دانشمندان مورد مطالعه و پیگیری است.
مدارک به دست آمده از دو هزارسال قبل از میلاد در یکی از اهرام مصر نیز که در یکی از اطاق ها تصویری به دست آمده، حاکی از مطالعه این نسبت روی اجزای بدن انسان است که مطالعه آن توسط لوکوربوزیه معمار فرانسوی روی بدن انسان، جدول معروفی را به دست می دهد که با استفاده از قابلیت تقسیم طبیعی در بدن انسان، علم نسبت ها را در ساختمان وارد کرده است. بررسی های لوکوربوزیه بعد از وی توسط دیگر دانشمندان مورد مطالعه و پیگیری است.
لئوناردو داوینچی در ترسیم نقاشی معروف خود از بدن انسان از نسبت طلایی بهره گرفته است. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
نسبت قد انسان به فاصله ناف تا پاشنه پا.
نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج.
نسبت فاصله شانه تا بالای سر به اندازه سر.
نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر.
نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا.
انتخاب ده ضلعی منتظم از طرف هنرمندان ایرانی و استفاده آن در کارهای معماری (پوشش گنبدها با کاربندی ده) و کارهای هنری (گره سازی ها که پایه آنها روی ده ضلعی منتظم قرار دارد) توجه و دقت آنها و بالاخره دید آنها را در انتخاب و به دست آوردن بهترین تناسبات در خطوط و سطوح را می رساند. چرا که در ده ضلعی منتظم نسبت شعاع به طول ضلع، همان نسبت طلائی است که در تمام کاربندی پوشش های گنبدی در معماری اصیل ایرانی - اسلامی از آن استفاده شده است.
همچنین مثلث متساوی الساقینی که ابوالوفاء بوزجانی در کشیدن پنج ضلعی از آن استفاده کرده و آن را مثلث پنج ضلعی نامیده است، مثلثی است که بین ساق و قاعده آن این نسبت طلایی وجود دارد.
در مطالعه در طبیعت نیز این تناسب زیاد دیده می شود نظیر فاصله برگ های روی ساقه و ساقه روی شاخه و شاخه روی تنه در بعضی گیاهان که بین هر دو زوج، سومی تقریبا در جای طلایی قرار گرفته است.

پوسته مارپیچی یک حلزون نمونه ای ساده و درعین حال زیبا از نسبت طلائی است.
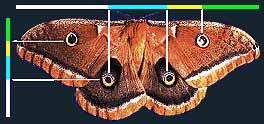
نسبت طلایی در فواصل خال های پروانه

نسبت طلائی در فواصل افقی قطعات ویولون

رعایت نسبت طلایی در طول و عرض iPod نسبت به محصولات مشابه
لیست آثار هنری طراحی شده با توجه به نسبت طلائی:
http://en.wikipedia.org/wiki/List_of_works_designed_with_golden_ratio
روابط ریاضی حاکم بر عدد طلائی:
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/phi.html
[ دوشنبه 92/9/11 ] [ 12:7 عصر ] [ علیرضا حسینی ]
مرد ویتورین
مرد ویتورین یا مرد ویترُویَن (به ایتالیایی Uomo vitruviano) یک طراحی از لئوناردو داوینچی است که به احتمال زیاد در 1487 کشیده شده[1] و طرحی تمامقد از معمار ایتالیایی ویترویوس است. این طراحی که با جوهر بر روی کاغذ کشیده شده بدن برهنه مردی را در دو حالت مختلف نشان می دهد که همزمان درون یک دایره و مربع محاط شده اند. این طراحی در ونیز ایتالیا نگهداری شده و جز در مواقع خاص به نمایش درنمیآید[2][3]
مطابق مشاهدات لئوناردو داوینچی در متن تصویر که به صورت قرینه نوشته شده است، نقاشی به عنوان توصیفی از تناسب های موجود در بدن انسان مذکر در غالب بدن ویترویوس کشیده شده است :
- کف دست به پهنای 4 انگشت است.
- کف پا به پهنای 4 کف دست است.
- اندازه نوک انگشتان دست تا آرنج، 6 برابر پهنای کف دست است.
- قد یک مرد، به اندازه 4 آرنج است (یعنی 24 کف دست).
- همچنین قد انسان به اندازه دستهای باز شده اوست.
- فاصله مبان رستنگاه مو تا پایی چانه، برابر یک دهم قد انسان است.
- فاصله میان روی سر تا پایی چانه، برابر یک هشتم قد انسان است.
- فاصله میان پشت گردن تا رستنگاه مو از جلو، برابر یک ششم قد انسان است.
- حداکثر عرض شانه انسان، برابر یک چهارم قد اوست (یک آرنج).
- فاصله میان وسط سینه تا بالای سر، یک چهارم قد انسان است(یک آرنج).
- فاصله میان آرنج تا زیربغل، یک هشتم قد انسان است (نصف آرنج).
- طول دست (از انتهای مچ تا سر انگشتان)، یک دهم قد انسان است.
- فاصله از پایین چانه تا بینی، برابر یک سوم طول صورت است.
- فاصله از رستنگاه مو تا ابرو، برابر یک سوم طول صورت است.
- اندازه گوش، برابر نصف طول صورت است.
- اندازه پای انسان، یک ششم قد اوست.
نسبت طلائی
بر خلاف بعضی از نظریات، در متن مرد ویتورین?اثر لئوناردو داوینچی اشارهای به نسبت طلایی نشده است، هرچند چندین نسبت دیگر در آن آورده شدهاند.[4][5]
منابع
- پرش به بالا ↑ در ویکیپدیای آلمانی سال 1493 ذکر گردیده شدهاست.،
- پرش به بالا ↑ The Vitruvian man
- پرش به بالا ↑ Da Vinci"s Code
- پرش به بالا ↑ Donald E. Simanek. "Fibonacci Flim-Flam". Archived from the original on 2012-08-05. Retrieved April 9, 2013.
- پرش به بالا ↑ "Part of the process of becoming a mathematics writer is, it appears, learning that you cannot refer to the golden ratio without following the first mention by a phrase that goes something like "which the ancient Greeks and others believed to have divine and mystical properties. " Almost as compulsive is the urge to add a second factoid along the lines of "Leonardo Da Vinci believed that the human form displays the golden ratio. " There is not a shred of evidence to back up either claim, and every reason to assume they are both false. Yet both claims, along with various others in a similar vein, live on." Keith Devlin (May 2007). "The Myth That Will Not Go Away". Archived from the original on 2012-08-04. Retrieved April 10, 2013.
- ویکیپدیای انگلیسی-بازدید در 30 مه 2010
نگارخانه
[ دوشنبه 92/9/11 ] [ 12:1 عصر ] [ علیرضا حسینی ]
نسبت طلایی
نسبت طلایی یا عدد فی (به انگلیسی: Golden ratio) در ریاضیات و هنر هنگامی است که «نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر» باشد.[1]»
تعریف دیگر نسبت طلایی این است که «عددی مثبت است که اگر به آن یک واحد اضافه کنیم به مربع آن خواهیم رسید». تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد.
محتویات
عدد فی
بسیاری از مراجع علمی، حرف یونانی  یا عدد فی را برای این عدد انتخاب کردهاند. مقدار عددی عدد طلایی برابر به طور تقریبی برابر است با:
یا عدد فی را برای این عدد انتخاب کردهاند. مقدار عددی عدد طلایی برابر به طور تقریبی برابر است با:
تعبیر هندسی دیگر اینگونهاست: پاره خط AB و نقطه? M روی آن مفروضند به گونهای که نسبت a به b برابر است با نسبت a+b به a. این نسبت برابر φ است. یعنی:
عدد فی با تعداد اعشار بیشتر
عدد فی با تعداد اعشار بیشتر به شرح زیر است.[2]
1?61803398874989484820458683436563811772030917980576286213544862270526046281890 244970720720418939113748475408807538689175212663386222353693179318006076672635 443338908659593958290563832266131992829026788067520876689250171169620703222104 321626954862629631361443814975870122034080588795445474924618569536486444924104 432077134494704956584678850987433944221254487706647809158846074998871240076521 705751797883416625624940758906970400028121042762177111777805315317141011704666 599146697987317613560067087480710131795236894275219484353056783002287856997829 778347845878228911097625003026961561700250464338243776486102838312683303724292 675263116533924731671112115881863851331620384005222165791286675294654906811317 159934323597349498509040947621322298101726107059611645629909816290555208524790 352406020172799747175342777592778625619432082750513121815628551222480939471234 145170223735805772786160086883829523045926478780178899219902707769038953219681 986151437803149974110692608867429622675756052317277752035361393621076738937645 560606059216589466759551900400555908950229530942312482355212212415444006470340 565734797663972394949946584578873039623090375033993856210242369025138680414577 995698122445747178034173126453220416397232134044449487302315417676893752103068 737880344170093954409627955898678723209512426893557309704509595684401755519881 921802064052905518934947592600734852282101088194644544222318891319294689622002 301443770269923007803085261180754519288770502109684249362713592518760777884665 836150238913493333122310533923213624319263728910670503399282265263556209029798 642472759772565508615487543574826471814145127000602389016207773224499435308899 909501680328112194320481964387675863314798571911397815397807476150772211750826 945863932045652098969855567814106968372884058746103378105444390943683583581381 131168993855576975484149144534150912954070050194775486163075422641729394680367 319805861833918328599130396072014455950449779212076124785645916160837059498786 006970189409886400764436170933417270919143365013715766011480381430626238051432...
پیشینه
پیشینه توجه به عدد طلایی نه به زمان فیبوناچی بلکه به زمانهای بسیار دورتر میرسد.اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کردهاست. لوکا پاچیولی در سال 1509 میلادی کتابی با عنوان نسبت الهی (The Divine Proportion) تالیف کرد. وی در آن نقاشیهایی از لئوناردو داوینچی آوردهاست که پنج جسم افلاطونی را نمایش میدهند و در آنها نیز به این نسبت اشاره شدهاست.
مصریان، سالها قبل از میلاد از این نسبت آگاه بودهاند و آن را در ساخت اهرام مصر رعایت کردهاند. بسیاری از الگوهای طبیعی در بدن انسان این نسبت را دارا هستند. نسبت طول ضلع پنج پر منتظم به طول ضلع پنج ضلعی منتظم برابر همین عدد است. روانشناسان هم بر این باورند زیباترین مستطیل به دید انسان، مستطیلی است که نسبت طول به عرض آن برابر عدد طلایی باشد.
طبیعت
لئوناردو داوینچی اولین کسی بود که نسبت دقیق استخوانهای انسان را اندازه گیری نمود و ثابت کرد که این تناسبات با ضریب عدد طلایی هستند.
نسبت طلایی در ایران
برج و میدان آزادی:طول بنا 63 و عرض ان 42 است که 5/1=42: 63 و به عدد طلایی نزدیک میباشدسبک معماری آن نیزطاق بزرگی است که تلفیقی از سبک هخامنشی و ساسانی و اسلامی است که منحنی آن با الهام از طاق کسری معماری ایران باستان را تداعی مینماید.
قلعه دالاهو، کرمانشاه:خطی از استحکامات به طول دو و نیم کیلومتر و عرض چهار متر با قلوه و لاشه سنگ به همراه ملات دیوار گچ را میسازد. سرتاسر نمای خارجی این دیوار با مجموعهای از برجهای نیم دایرهای شکل تقویت شده است. می دانیم6/1=5/2: 4 که همان عدد طلایی است.
بیستون از دوره هخامنشی، کرمانشاه:به طول 5 کیلومتر و عرض 3 کیلومتراست. اعداد5و3هردوجزودنباله فیبوناتچی هستندو6/1=5:3 و ابعاد برجسته کاری 18 در 10 پاست که قامت "داریوش"5 پا و 8 اینچ (170 سانتیمتر) بلندی داردکه هر دو اعداد فیبوناتچی هستند.
یکی از هنرهای معماری در تخت جمشید این است که نسبت ارتفاع سر درها به عرض آنها و همین طور نسبت ارتفاع ستونها به فاصله? بین دو ستون نسبت طلایی است. نسبت طلایی نسبت مهمی در هندسه است که در طبیعت وجود دارد. این نشانگر هنر ابرانیان باستان در معماری است.
پل ورسک در مازندران: این پل بر روی رودخانه ورسک در مجاورت سواد کوه بنا شد. بلندی این پل 110 متر است وطول قوس آن 66 متر میباشد(6/1 = 66: 110).
مقبره ابن سینا:آرامگاه دروسط تالاری مربع شکل قرارگرفته که پله مدور (مارپیچ فیبوناتچی) و پایههای دوازده گانه برج را احاطه کردهاند. سطح حیاط باسه پله سراسری به ایوان متصل است. ایوان با دری به ارتفاع 2/3 متر و عرض 9/1 متر به سرسرای آرامگاه متصل است (6/1=9/1: 2/3)در دو طرف سرسرا دو تالار قرار دارد یکی در جنوب که تالار سخنرانی و اجتماعات است. و یکی در شمال که کتابخانه آرامگاه است. طول تالار کتابخانه 45/9 متر وعرض آن 75/5 متر است(6/1=75/5: 45/9)
ارگ بم:این بنا 300 متر طول و 200 متر عرض داشته و از 2 قسمت تشکیل شده است. این دژ 5 شیوه ساختاری از خشت خام دارد. (3 و 2 و 5 اعداد دنباله فیبوناتچی هستند)
میدان نقش جهان و مسجد لطف الله:در کتب اخیر، نویسنده جیسون الیوت بر این باور است که نسبت طلایی توسط طراحان میدان نقش جهان و در مجاورت مسجد لطف الله مورد استفاده قرار گرفته است.[3]
عدد فی و معماری اسلامی
گفته میشود که: "اگر فاصله کعبه را در شهر مکه تا قطب شمال و جنوب اندازه گرفته و به هم تقسیم کنید عدد فی بدست خواهد آمد. برای اطمینان میتوانید از نرمافزار Google Earth استفاده کنید و به این حقیقت دست یابید." کعبه در لتیتودِ 21?4224945 میباشد که به تناسبِ (90-21?4224945)/(90+21?4224945) برابر با 1?62476739 میباشد که با عددِ فی تطابق دارد.
تاکنون نه تنها در کتاب رمز داوینچی بلکه پیامها، اسرار مذهبی و کهن در دیوارهای زیارتگاههای اسلامی به صورت رمز قرار مشاهده شده است. بسیاری از کاشیکاریهای بناهای اسلامی متعلق به ? 500?سال پیش توانستهاند الگوهای فراوان ریاضی پیدا کنند که تا دهه ?1970? برای غربیها ناشناخته بوده است. اساس یک طراحی هندسی برای نشان دادن یک نماد از علم " ماندالا" است که به عقیده بسیاری از ملت شرق به تعمق و اندیشه کمک میکند خلق بسیاری از نامحدودها با استفاده از مثلث و مستطیل طلایی از این گونه است
کیث کریچلو" ? keith Critchlow?نویسنده کتاب "الگوهای ریاضی اسلامی" چنین ادعا میکند: ما دریافتهایم که اسلام در دوره قرون وسطی تا چه اندازه پیشرفته بوده است. نام این الگوهای ریاضی پیچیده در آن دوران "شیمی بیضی متقارن ممنوعه" مینامند. آنها از الگوی کاشیهای هرمی برخوردارند و با چرخش یک سوم در آن قابل شناسایی هستند. همین قانون برای کاشیهای مستطیلی نیز پیروی میکند که با چرخش یک چهارم قابل شناسایی هستند ما برای کاشیهای شش گوش چرخش یک ششم لازم است. اما این شبکهها بدون وجود پنجضلعیها کامل نمیشوند و بدون رعایت فاصله میان آنها در کنار هم جفت نمیشوند و نمیتوان آنها را با با چرخش یک پنجم در کنار هم قرار داد. آقای لو توانست در دیوار یکی از زیارتگاههای ایران دو نوع از این کاشیکاریها بزرگ را که با کاشیهای همشکل ساخته شده بود، کشف کند به گونهای که ظاهراً از نسبت طلایی فیثاغورثی تبعیت میکردند. کریچلو در اینباره میگوید: سازندگان بنا بطور حتم از این نسبت خبر داشتند.
در سال ? 1973?سر "راجر پنروس" ? Roger Penrose?ریاضیدان برجسته غربی توانست با در نظر گرفتن این پنجضلعیها الگویی پنج تایی با شکلی بسازد که از آن به عنوان کیت و یا دارت نام برده میشود. او نخستین غربی بود که این حساب را کشف کرد و در آن زمان گمان میکرد نخستین کسی است به این موضوع پی بردهاست. خلاقیت وی به خلق خواص ریاضیاتی منجر شد هر دسته میتواند حاوی تعداد مشخصیاز کیتها و دارتهایی باشد که میتوانند تا بینهایت و بدون تکرارپذیری الگوهای کوچکتری از کیتها و دارتها بسازند. هر چقدر تعداد این اشکال ریز افزایش پیدا کند آنگاه نسبت کیتها به دارتها به نسبتی موسوم به "نسبت طلایی" میرسد.
"گلرو نجیب اوغلو" ? Gulru Nacipoglu?یکی از اساتید دانشگاه هاروارد میگوید: خلقت انسان مشابه هم است و شکل مشخصی دارد که از عجایب خلقت خداوندی است این که این الگوها به کجا ختم میشوند و به صورت هوشمندانهای در درها و پنجرهها به کار رفتهاند مسئلهای است که نمیتوان مشخص کرد. به گفته وی، با وجود این که الگوی پنروس به قرن ? 14?یا ? 15?بازمیگردد اما این اشکال کاشیکاری در دنیای اسلام از صدها سال قبل از آن به کار گرفته شده است. در منبتکاریهای ایران در قرن پانزدهم و اوایل شانزدهم فهرستی از بسیاری از این طرحها قرار دارند که ممکن است سرنخی برای شکوه ریاضیات اسلامی در مساجد ایران و ترکیه و مدارس بغداد و زیارتگاههای هند و افغانستان باشد. دانشمندان اکنون میدانند که مسلمانان در آن دوران میتوانستند معادلات جبری به توان ? 3?و فراتر از آن را حل کنند معادلاتی که بسیار دشوارتر از معادله دو مجهولی است و اساس جبر به شمار میرود. مسلمانان همچنین دارای حسابگرهای مکانیکی بودند و در علم داروشناسی و ستاره شناسی پیشرفتهتر از اروپاییها بودهاند اما با این حال جای تاسف است که تعداد اندکی از این دانشمندان درباره یافتههای خود کتاب و یا اثر به رشته تحریر درآوردهاند".
ترسیم
برای رسم کردن مستطیل طلایی ابتدا مربع ABCD با استفاده از ضلع کوچک رسم میشود. سپس ضلع AB را نصف کرده، از وسط آن (نقطه G) با پرگار یک قوس به شعاع GC ترسیم کرده و ضلع بزرگ مستطیل (AE) را به دست میآورند. با توجه به شکل ترسیم شده، نصف طول این ضلع برابر نسبت طلایی است.[1]
محاسبات
برای بدست آوردن نسبت طلائی از تعریف هندسی آن استفاده میکنیم:
از این معادله که تعریف عدد  است، که از معادله سمت راست میتوان نتیجه گرفت:
است، که از معادله سمت راست میتوان نتیجه گرفت:  ، پس خواهیم داشت:
، پس خواهیم داشت:
با حذف b از طرفین به دست میآید:
پس از ساده سازی این معادله، معادله درجه دومی بر حسب  به دست میآید:
به دست میآید:
و پاسخ مثبت آن:
که همان نسبت طلائی است.
جستارهای وابسته
پانویس
- ↑ پرش به بالا به: 1?0 1?1 عبدالمجید حسینیراد، ص.72
- پرش به بالا ↑ http://www.cs.arizona.edu/icon/oddsends/phi.htm
- پرش به بالا ↑ Jason Elliot (2006). "Mirrors+of+the+Unseen"+golden-ratio+maidan Mirrors of the Unseen: Journeys in Iran. Macmillan. pp. 277, 284. ISBN 978-0-312-30191-0.
منابع
- حسینیراد، عبدالمجید. مبانی هنرهای تجسمی (قسمت اول). شرکت چاپ و نشر کتابهای درسی ایران، 1382. ص.72.
- Jason Elliot (2006). "Mirrors+of+the+Unseen"+golden-ratio+maidan Mirrors of the Unseen: Journeys in Iran. Macmillan. pp. 277, 284. ISBN 978-0-312-30191-0.
[ دوشنبه 92/9/11 ] [ 11:55 صبح ] [ علیرضا حسینی ]
هنر خام
اصطلاح هنر خام (به انگلیسی Art Brut یا هنرخام) را ژان دوبوفه Jean Dubuffet ، نقاش برجسته فرانسوی بعد از جنگ جهانی دوم، در مورد هنر کسانی به کار برد که خارج از شمول جامعه متعارف هنری قرار داشتند. یعنی نقاشی هاو خط خطی کردنهای بیماران روانی، زندانیان، کودکان، انسانهای ابتدایی و خام دست، و امثال آنها. همان گونه که کوبیستها در مراحل نخستین آفرینشهای خوداز مجسمههای بومیان اقیانوسیه و افریقا الهام گرفتند، دوبوفه توانست از مطالعه هنرهای پیش گفته برای آفرینش کارهای خود الهام بگیرد. وی معتقد بود که این نوع نقاشی برخاسته از ابتکار خالص بوده و بیشترین توانایی را برای به نمایش درآوردن عواطف و ارزشهای انسانی حائز است. او هنر خام را از هنر ناایو Naive Art (هنر ابتدایی یا کودک گونه) متفاوت میداند، به این دلیل که این هنرمندان، آثارشان را برای استفاده خودشان و ارائه شخصی بوجود میآورند. درحالیکه نقاشان ناایو در جریان نقاشی معقول باقی میمانند و به منظور شناخت عمومی (اسقبال مردم و یا دولت) فعالیت میکنند.
محتویات
تاریخچه
دوبوفه در سال 1945 گردآوری آثاری آزاد از قید ضوابط فرهنگی و یا جهت گیریهای سنتی و مرسوم را آغاز کرد و در سال 1948 به همراه آندره برتون شاعر فرانسوی و دیگران the Compagnie d’Art Brut را بنا نهاد. بخش بزرگی از کلکسیون دوبوفه، آثار بیماران روانی را در برداشت. در سال 1972 مجموعه اش را که شامل بیش از پنج هزار اثر بود به شهرداری شهر لوزان سوئیس اهدا کرد. چهار سال بعد نمایشگاهی از این آثار در همان شهر افتتاح شد. برخی از آثار دوبوفه (نقاشیها و مجسمهها) که حاصل تقلید مستقیم از Art Brut است، نقدها و موفقیتهای تجاری به دنبال داشتند.
پیشزمینه و انگیزهها
گفته شدهاست که مهم ترین منبع الهام بخش دوبوفه در این خصوص، کتاب دیوانگان نگارش هانس پرینتسهورن، روانکاو سوئیسی بودهاست.
منابع
لینتن، نوربرت. هنر مدرن. ترجمه علی رامین. چاپ چهارم. تهران: نی.1388
[ دوشنبه 92/9/11 ] [ 10:30 صبح ] [ علیرضا حسینی ]
نمونه کارهای رابرت اسمیتسون
در کارهای ارائه شده در طبیعت او با استفاده از مواد آلی و نشان دادن تاثیر آن بر زمین حرکت نوینی را آغاز کرد.
ASPHALT RUNDOWN,rome,italy,1969
GLUE POUR,vancouver,canada,1969
SPIRAL JETTY,rozel point,great salt lake.uta 1970





1964

1965

1965

1965

1965
1966

1966

1966

1966

1967
1967

1968

1968

1968

1968
1969

1969

1969

1970

1973

1997











[ دوشنبه 92/9/11 ] [ 10:22 صبح ] [ علیرضا حسینی ]
رابرت اسمیتسون
رابرت اسمیتسون (1938-1973) مجسمه ساز، مقاله نویس و فیلمساز آمریکایی است. او به عنوان یک هنرمند زیست محیطی شناخته شده استآثاری که در دل طبیعت و از خود آن هستند..
مجسمه ساز رابرت اسمیتسون کار خود را به عنوان یک نقاش آغاز کرد. در نیوجرسی ، در تاریخ 2 ژانویه 1938 متولد شده.اسمیتسون در مدارس عمومی جرسی تحصیل کرد. در مدرسه عالی کلیفتون او برنده یک بورس تحصیلی برای شرکت در کلاس های شبانه ی در کالج دانشجویان هنر شد. در سال 1956 او در مدرسه موزه ی بروکلین آموزش دید. پس از فارغ التحصیلی از دبیرستان در سال 1957 برای خدمت به ارتش به شهر نیویورک نقل مکان کرد. او اولین اثر خود را در سبک اکسپرسیونیستی در قالب نقاشی ارائه کرد.
او در دوران کودکی به طبیعت علاقه مند شده بود. او در خانه اش در نیوجرسی کلکسیونی از خزندگان و فسیل های آن ها داشت. او در دبیرستان به تعداد زیادی از موزه های طبیعی نیویورک رفته بود، جایی که او مجذوب دایناسورها شد. نانسی هولت یکی از هنرمندان، وقتی علاقه او را به زیست شناسی و طبیعت دید، او را به مجسمه سازی تشویق کرد. در طبیعت او شروع به جمع آوری نمونه ها کرد به عنوان مثال، اسفنج ها و یا مواد دیگر را در قالب هنری در طبیعت نمایش داد که نشان می دهد این بود که هنر، مانند زیست شناسی، یک ماده خنثی است در طبیعت که می تواند به برقراری روابط معنی دار و سازمان یافته دست پیدا کند.
[ دوشنبه 92/9/11 ] [ 10:15 صبح ] [ علیرضا حسینی ]
رابرت اسمیتسون
رابرت اسمیتسون هنرمند آمریکایی است که برای کار در هنر زمینی مشهور شد.
اسکله حلزونی
اسمیتسون اسکله حلزونی را در سال 1970 ساخت. این اثر در واقع جادهای سنگی است، که از کنار ساحل تپهای حرکت و در کرانه برکه بزرگ نمک در خلیج یوتا به صورت مارپیچ یک حلزون شکل میگیرد، به نحوی که شکل اسپیرال به طور کامل از ارتفاع بالای زمین قابل رویت است. نکته جالب توجه دراین پروژه، این است که؛ مکان آن تدریجاً در حال حرکت است. چون سطح آب برکه بالا آمده و جاده را در بر میگیرد. بنابر این کل اثر در حال حاضر تنها به مدد عکسها قابل شناسایی است و چهره امروزیش به کلی نسبت به چهره اولیه دگرگون شدهاست.
منابع
- لوسی اسمیت. ادوارد.مفاهیم و رویکردهادراخرین جنبشهای هنری قرن بیستم.دکتر علیرضا سمیع اذرنشر نظر.چاپ هفتم تهران 1387
[ دوشنبه 92/9/11 ] [ 10:11 صبح ] [ علیرضا حسینی ]
::