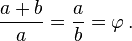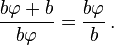نسبت طلایی
نسبت طلایی یا عدد فی (به انگلیسی: Golden ratio) در ریاضیات و هنر هنگامی است که «نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر» باشد.[1]»
تعریف دیگر نسبت طلایی این است که «عددی مثبت است که اگر به آن یک واحد اضافه کنیم به مربع آن خواهیم رسید». تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد.
محتویات
عدد فی
بسیاری از مراجع علمی، حرف یونانی  یا عدد فی را برای این عدد انتخاب کردهاند. مقدار عددی عدد طلایی برابر به طور تقریبی برابر است با:
یا عدد فی را برای این عدد انتخاب کردهاند. مقدار عددی عدد طلایی برابر به طور تقریبی برابر است با:
تعبیر هندسی دیگر اینگونهاست: پاره خط AB و نقطه? M روی آن مفروضند به گونهای که نسبت a به b برابر است با نسبت a+b به a. این نسبت برابر φ است. یعنی:
عدد فی با تعداد اعشار بیشتر
عدد فی با تعداد اعشار بیشتر به شرح زیر است.[2]
1?61803398874989484820458683436563811772030917980576286213544862270526046281890 244970720720418939113748475408807538689175212663386222353693179318006076672635 443338908659593958290563832266131992829026788067520876689250171169620703222104 321626954862629631361443814975870122034080588795445474924618569536486444924104 432077134494704956584678850987433944221254487706647809158846074998871240076521 705751797883416625624940758906970400028121042762177111777805315317141011704666 599146697987317613560067087480710131795236894275219484353056783002287856997829 778347845878228911097625003026961561700250464338243776486102838312683303724292 675263116533924731671112115881863851331620384005222165791286675294654906811317 159934323597349498509040947621322298101726107059611645629909816290555208524790 352406020172799747175342777592778625619432082750513121815628551222480939471234 145170223735805772786160086883829523045926478780178899219902707769038953219681 986151437803149974110692608867429622675756052317277752035361393621076738937645 560606059216589466759551900400555908950229530942312482355212212415444006470340 565734797663972394949946584578873039623090375033993856210242369025138680414577 995698122445747178034173126453220416397232134044449487302315417676893752103068 737880344170093954409627955898678723209512426893557309704509595684401755519881 921802064052905518934947592600734852282101088194644544222318891319294689622002 301443770269923007803085261180754519288770502109684249362713592518760777884665 836150238913493333122310533923213624319263728910670503399282265263556209029798 642472759772565508615487543574826471814145127000602389016207773224499435308899 909501680328112194320481964387675863314798571911397815397807476150772211750826 945863932045652098969855567814106968372884058746103378105444390943683583581381 131168993855576975484149144534150912954070050194775486163075422641729394680367 319805861833918328599130396072014455950449779212076124785645916160837059498786 006970189409886400764436170933417270919143365013715766011480381430626238051432...
پیشینه
پیشینه توجه به عدد طلایی نه به زمان فیبوناچی بلکه به زمانهای بسیار دورتر میرسد.اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کردهاست. لوکا پاچیولی در سال 1509 میلادی کتابی با عنوان نسبت الهی (The Divine Proportion) تالیف کرد. وی در آن نقاشیهایی از لئوناردو داوینچی آوردهاست که پنج جسم افلاطونی را نمایش میدهند و در آنها نیز به این نسبت اشاره شدهاست.
مصریان، سالها قبل از میلاد از این نسبت آگاه بودهاند و آن را در ساخت اهرام مصر رعایت کردهاند. بسیاری از الگوهای طبیعی در بدن انسان این نسبت را دارا هستند. نسبت طول ضلع پنج پر منتظم به طول ضلع پنج ضلعی منتظم برابر همین عدد است. روانشناسان هم بر این باورند زیباترین مستطیل به دید انسان، مستطیلی است که نسبت طول به عرض آن برابر عدد طلایی باشد.
طبیعت
لئوناردو داوینچی اولین کسی بود که نسبت دقیق استخوانهای انسان را اندازه گیری نمود و ثابت کرد که این تناسبات با ضریب عدد طلایی هستند.
نسبت طلایی در ایران
برج و میدان آزادی:طول بنا 63 و عرض ان 42 است که 5/1=42: 63 و به عدد طلایی نزدیک میباشدسبک معماری آن نیزطاق بزرگی است که تلفیقی از سبک هخامنشی و ساسانی و اسلامی است که منحنی آن با الهام از طاق کسری معماری ایران باستان را تداعی مینماید.
قلعه دالاهو، کرمانشاه:خطی از استحکامات به طول دو و نیم کیلومتر و عرض چهار متر با قلوه و لاشه سنگ به همراه ملات دیوار گچ را میسازد. سرتاسر نمای خارجی این دیوار با مجموعهای از برجهای نیم دایرهای شکل تقویت شده است. می دانیم6/1=5/2: 4 که همان عدد طلایی است.
بیستون از دوره هخامنشی، کرمانشاه:به طول 5 کیلومتر و عرض 3 کیلومتراست. اعداد5و3هردوجزودنباله فیبوناتچی هستندو6/1=5:3 و ابعاد برجسته کاری 18 در 10 پاست که قامت "داریوش"5 پا و 8 اینچ (170 سانتیمتر) بلندی داردکه هر دو اعداد فیبوناتچی هستند.
یکی از هنرهای معماری در تخت جمشید این است که نسبت ارتفاع سر درها به عرض آنها و همین طور نسبت ارتفاع ستونها به فاصله? بین دو ستون نسبت طلایی است. نسبت طلایی نسبت مهمی در هندسه است که در طبیعت وجود دارد. این نشانگر هنر ابرانیان باستان در معماری است.
پل ورسک در مازندران: این پل بر روی رودخانه ورسک در مجاورت سواد کوه بنا شد. بلندی این پل 110 متر است وطول قوس آن 66 متر میباشد(6/1 = 66: 110).
مقبره ابن سینا:آرامگاه دروسط تالاری مربع شکل قرارگرفته که پله مدور (مارپیچ فیبوناتچی) و پایههای دوازده گانه برج را احاطه کردهاند. سطح حیاط باسه پله سراسری به ایوان متصل است. ایوان با دری به ارتفاع 2/3 متر و عرض 9/1 متر به سرسرای آرامگاه متصل است (6/1=9/1: 2/3)در دو طرف سرسرا دو تالار قرار دارد یکی در جنوب که تالار سخنرانی و اجتماعات است. و یکی در شمال که کتابخانه آرامگاه است. طول تالار کتابخانه 45/9 متر وعرض آن 75/5 متر است(6/1=75/5: 45/9)
ارگ بم:این بنا 300 متر طول و 200 متر عرض داشته و از 2 قسمت تشکیل شده است. این دژ 5 شیوه ساختاری از خشت خام دارد. (3 و 2 و 5 اعداد دنباله فیبوناتچی هستند)
میدان نقش جهان و مسجد لطف الله:در کتب اخیر، نویسنده جیسون الیوت بر این باور است که نسبت طلایی توسط طراحان میدان نقش جهان و در مجاورت مسجد لطف الله مورد استفاده قرار گرفته است.[3]
عدد فی و معماری اسلامی
گفته میشود که: "اگر فاصله کعبه را در شهر مکه تا قطب شمال و جنوب اندازه گرفته و به هم تقسیم کنید عدد فی بدست خواهد آمد. برای اطمینان میتوانید از نرمافزار Google Earth استفاده کنید و به این حقیقت دست یابید." کعبه در لتیتودِ 21?4224945 میباشد که به تناسبِ (90-21?4224945)/(90+21?4224945) برابر با 1?62476739 میباشد که با عددِ فی تطابق دارد.
تاکنون نه تنها در کتاب رمز داوینچی بلکه پیامها، اسرار مذهبی و کهن در دیوارهای زیارتگاههای اسلامی به صورت رمز قرار مشاهده شده است. بسیاری از کاشیکاریهای بناهای اسلامی متعلق به ? 500?سال پیش توانستهاند الگوهای فراوان ریاضی پیدا کنند که تا دهه ?1970? برای غربیها ناشناخته بوده است. اساس یک طراحی هندسی برای نشان دادن یک نماد از علم " ماندالا" است که به عقیده بسیاری از ملت شرق به تعمق و اندیشه کمک میکند خلق بسیاری از نامحدودها با استفاده از مثلث و مستطیل طلایی از این گونه است
کیث کریچلو" ? keith Critchlow?نویسنده کتاب "الگوهای ریاضی اسلامی" چنین ادعا میکند: ما دریافتهایم که اسلام در دوره قرون وسطی تا چه اندازه پیشرفته بوده است. نام این الگوهای ریاضی پیچیده در آن دوران "شیمی بیضی متقارن ممنوعه" مینامند. آنها از الگوی کاشیهای هرمی برخوردارند و با چرخش یک سوم در آن قابل شناسایی هستند. همین قانون برای کاشیهای مستطیلی نیز پیروی میکند که با چرخش یک چهارم قابل شناسایی هستند ما برای کاشیهای شش گوش چرخش یک ششم لازم است. اما این شبکهها بدون وجود پنجضلعیها کامل نمیشوند و بدون رعایت فاصله میان آنها در کنار هم جفت نمیشوند و نمیتوان آنها را با با چرخش یک پنجم در کنار هم قرار داد. آقای لو توانست در دیوار یکی از زیارتگاههای ایران دو نوع از این کاشیکاریها بزرگ را که با کاشیهای همشکل ساخته شده بود، کشف کند به گونهای که ظاهراً از نسبت طلایی فیثاغورثی تبعیت میکردند. کریچلو در اینباره میگوید: سازندگان بنا بطور حتم از این نسبت خبر داشتند.
در سال ? 1973?سر "راجر پنروس" ? Roger Penrose?ریاضیدان برجسته غربی توانست با در نظر گرفتن این پنجضلعیها الگویی پنج تایی با شکلی بسازد که از آن به عنوان کیت و یا دارت نام برده میشود. او نخستین غربی بود که این حساب را کشف کرد و در آن زمان گمان میکرد نخستین کسی است به این موضوع پی بردهاست. خلاقیت وی به خلق خواص ریاضیاتی منجر شد هر دسته میتواند حاوی تعداد مشخصیاز کیتها و دارتهایی باشد که میتوانند تا بینهایت و بدون تکرارپذیری الگوهای کوچکتری از کیتها و دارتها بسازند. هر چقدر تعداد این اشکال ریز افزایش پیدا کند آنگاه نسبت کیتها به دارتها به نسبتی موسوم به "نسبت طلایی" میرسد.
"گلرو نجیب اوغلو" ? Gulru Nacipoglu?یکی از اساتید دانشگاه هاروارد میگوید: خلقت انسان مشابه هم است و شکل مشخصی دارد که از عجایب خلقت خداوندی است این که این الگوها به کجا ختم میشوند و به صورت هوشمندانهای در درها و پنجرهها به کار رفتهاند مسئلهای است که نمیتوان مشخص کرد. به گفته وی، با وجود این که الگوی پنروس به قرن ? 14?یا ? 15?بازمیگردد اما این اشکال کاشیکاری در دنیای اسلام از صدها سال قبل از آن به کار گرفته شده است. در منبتکاریهای ایران در قرن پانزدهم و اوایل شانزدهم فهرستی از بسیاری از این طرحها قرار دارند که ممکن است سرنخی برای شکوه ریاضیات اسلامی در مساجد ایران و ترکیه و مدارس بغداد و زیارتگاههای هند و افغانستان باشد. دانشمندان اکنون میدانند که مسلمانان در آن دوران میتوانستند معادلات جبری به توان ? 3?و فراتر از آن را حل کنند معادلاتی که بسیار دشوارتر از معادله دو مجهولی است و اساس جبر به شمار میرود. مسلمانان همچنین دارای حسابگرهای مکانیکی بودند و در علم داروشناسی و ستاره شناسی پیشرفتهتر از اروپاییها بودهاند اما با این حال جای تاسف است که تعداد اندکی از این دانشمندان درباره یافتههای خود کتاب و یا اثر به رشته تحریر درآوردهاند".
ترسیم
برای رسم کردن مستطیل طلایی ابتدا مربع ABCD با استفاده از ضلع کوچک رسم میشود. سپس ضلع AB را نصف کرده، از وسط آن (نقطه G) با پرگار یک قوس به شعاع GC ترسیم کرده و ضلع بزرگ مستطیل (AE) را به دست میآورند. با توجه به شکل ترسیم شده، نصف طول این ضلع برابر نسبت طلایی است.[1]
محاسبات
برای بدست آوردن نسبت طلائی از تعریف هندسی آن استفاده میکنیم:
از این معادله که تعریف عدد  است، که از معادله سمت راست میتوان نتیجه گرفت:
است، که از معادله سمت راست میتوان نتیجه گرفت:  ، پس خواهیم داشت:
، پس خواهیم داشت:
با حذف b از طرفین به دست میآید:
پس از ساده سازی این معادله، معادله درجه دومی بر حسب  به دست میآید:
به دست میآید:
و پاسخ مثبت آن:
که همان نسبت طلائی است.
جستارهای وابسته
پانویس
- ↑ پرش به بالا به: 1?0 1?1 عبدالمجید حسینیراد، ص.72
- پرش به بالا ↑ http://www.cs.arizona.edu/icon/oddsends/phi.htm
- پرش به بالا ↑ Jason Elliot (2006). "Mirrors+of+the+Unseen"+golden-ratio+maidan Mirrors of the Unseen: Journeys in Iran. Macmillan. pp. 277, 284. ISBN 978-0-312-30191-0.
منابع
- حسینیراد، عبدالمجید. مبانی هنرهای تجسمی (قسمت اول). شرکت چاپ و نشر کتابهای درسی ایران، 1382. ص.72.
- Jason Elliot (2006). "Mirrors+of+the+Unseen"+golden-ratio+maidan Mirrors of the Unseen: Journeys in Iran. Macmillan. pp. 277, 284. ISBN 978-0-312-30191-0.
[ دوشنبه 92/9/11 ] [ 11:55 صبح ] [ علیرضا حسینی ]